5.4 The Double Integral Over More General Regions
Our goal in this section is twofold: First, we wish to define the double integral of a function \(f(x,y)\) over regions \(D\) more general than rectangles; second, we want to develop a technique for evaluating this type of integral. To accomplish this, we shall define three special types of subsets of the \(xy\) plane, and then extend the notion of the double integral to them.
Elementary Regions
Suppose we are given two continuous real-valued functions \(\phi_1 \colon\, [a,b] \rightarrow {\mathbb R}\) and \(\phi_2\colon [a,b]\) \(\rightarrow\) \({\mathbb R}\) that satisfy \(\phi_1(x) \leq \phi_2(x)\) for all \(x \in [a,b]\). Let \(D\) be the set of all points \((x, y)\) such that \(x \in [a,b]\) and \(\phi_1(x) \leq y \leq \phi_2(x)\). This region \(D\) is said to be y-simple. Figure 5.20 shows various examples of \(y\)-simple regions. The curves and straight-line segments that bound the region together constitute the boundary of \(D\), denoted \(\partial \! D\). We use the phrase “\(y\)-simple” because the region is described in a relatively simple way, using \({y}\) as a function of \({x}\).
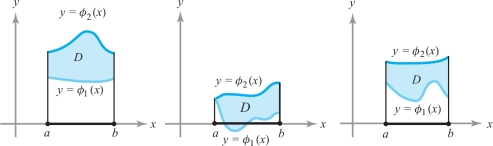
We say that a region \(D\) is x-simple if there are continuous functions \(\psi_1\) and \(\psi_2\) defined on \([c,d]\) such that \(D\) is the set of points \((x, y)\) satisfying \[ y \in [c,d\,] \hbox{and} \psi_1(y) \leq x \leq \psi_2(y), \] where \(\psi_1(y) \leq \psi_2(y)\) for all \(y \in [c,d]\). Again, the curves that bound the region \(D\) constitute its boundary \(\partial D\). Some examples of \(x\)-simple regions are shown in Figure 5.21. In this situation, \({x}\) is the distinguished variable, given as a function of \({y}\). Thus, the phrase \(x\)-simple is appropriate.
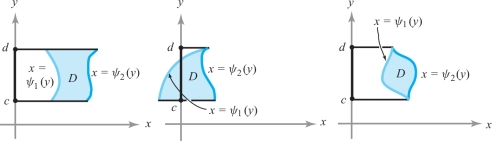
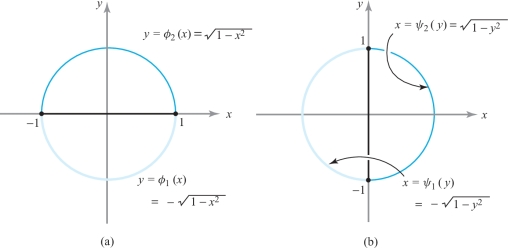
Finally, a simple region is one that is both \(x\)- and \(y\)-simple; that is, a simple region can be described as both an \(x\)-simple region and a \(y\)-simple region. An example of a simple region is a unit disk (see Figure 5.22).
284
Sometimes we will refer to any of the regions as elementary regions. Note that the boundary \(\partial\! D\) of an elementary region is the type of set of discontinuities of a function allowed in Theorem 2.
The Integral over an Elementary Region
We can now use an interesting “trick” to extend the definition of the integral from rectangles to elementary regions.
Definition: Integral over an Elementary Region
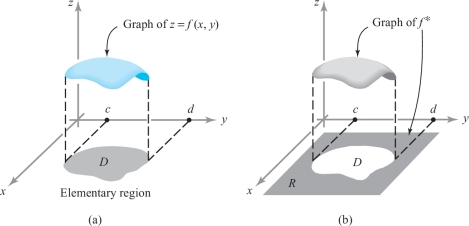
If \(D\) is an elementary region in the plane, choose a rectangle \(R\) that contains \(D\). Given \(f\colon D \rightarrow {\mathbb R}\), where \(f\) is continuous (and hence bounded), define \({\intop\!\!\!\intop}_D f(x,y)\, {\it dA}\), the integral of \(f\) over the set D, as follows: Extend \(f\) to a function \(f^*\) defined on all of \(R\) by \[ f^* (x,y) = \bigg\{ \begin{array}{lll} f(x,y) & \hbox{if} & (x,y)\in D\\[2pt] 0 & \hbox{if} & (x,y) \not\in D \hbox{ and } (x,y) \in R. \end{array} \]
Note that \(f^*\) is bounded (because \(f\) is) and continuous except possibly on the boundary of \(D\) (see Figure 5.23). The boundary of \(D\) consists of graphs of continuous functions, and so \(f^*\) is integrable over \(R\) by Theorem 2, Section 5.3. Therefore, we can define \[ \intop\!\!\!\intop\nolimits_{D}\, f(x,y)\ {\it dA} = \intop\!\!\!\intop\nolimits_{R} f^* (x,y)\ {\it dA}. \]
When \(f(x,y)\geq 0\) on \(D\), we can interpret the integral \({\intop\!\!\!\intop}_Df (x,y)\ {\it dA}\) as the volume of the three-dimensional region between the graph of \(f\) and \(D\), as is evident from Figure 5.23.
285
We have defined \({\intop\!\!\!\intop}_D f(x,y)\, {\it dx}\, {\it dy}\) by choosing a rectangle \(R\) that encloses \(D\). It should be intuitively clear that the value of \({\intop\!\!\!\intop}_D f(x,y)\, {\it dx}\, {\it dy} \) does not depend on the particular \(R\) we select; we shall demonstrate this fact at the end of this section.
Reduction to Iterated Integrals
If \(R=[a,b] \times [c,d]\) is a rectangle containing \(D\), we can use the results on iterated integrals in Section 5.3 to obtain \begin{eqnarray*} \intop\!\!\!\intop\nolimits_{D}\, f(x,y)\ {\it dA} = \intop\!\!\!\intop\nolimits_{R} \, f^* (x,y)\ {\it dA} &=& \int_a^b \int_c^d f^*(x,y)\ {\it dy}\, {\it dx}\\[6pt] &=&\int_c^d \int_a^b f^* (x,y)\ {\it dx}\, {\it dy}, \end{eqnarray*} where \(f^*\) equals \(f\) in \(D\) and zero outside \(D\), as before. Assume that \(D\) is a \(y\)-simple region determined by functions \(\phi_1\colon [a,b]\rightarrow {\mathbb R}\) and \(\phi_2\colon [a,b] \rightarrow{\mathbb R}\). Consider the iterated integral \[ \int_a^b\int_c^d f^* (x,y)\, {\it dy}\,{\it dx} \] and, in particular, the inner integral \(\int^d_c f^* (x,y)\, {\it dy}\) for some fixed \(x\) (Figure 5.24). By definition, \(f^*(x,y)=0\) if \(y<\phi_1(x)\) or \(y>\phi_2(x)\), so we obtain \[ \int_c^d f^*(x,y)\, {\it dy} =\int^{\phi_2(x)}_{\phi_1(x)} f^* (x,y)\, {\it dy} = \int^{\phi_2(x)}_{\phi_1(x)} f (x,y)\, {\it dy} . \]

286
We summarize what we have obtained in the following.
Theorem 4 Reduction to Iterated Integrals
If \(D\) is a \(y\)-simple region, as shown in Figure 5.24, then \begin{equation*} \intop\!\!\!\intop\nolimits_{D}f(x,y)\ {\it dA} = \int_a^b \int_{\phi_1(x)}^{\phi_2(x)} f(x,y)\, {\it dy}\,{\it dx}.\tag{1} \end{equation*}
In the case \(f(x, y) = 1\) for all \((x, y)\in D, {\intop\!\!\!\intop}_D f(x,y)\, {\it dA}\) is the area of \(D\). On the other hand, in this case, the right-hand side of formula (1) becomes: \[ \int^b_a \int^{\phi_2(x)}_{\phi_1(x)} f(x,y)\, {\it dy}\,{\it dx} = \int_a^b \, [\phi_2(x) - \phi_1(x)]\, {\it dx} = A(D) , \] which is the formula for the area of \(D\) learned in one-variable calculus. Thus, formula (1) checks in this case.
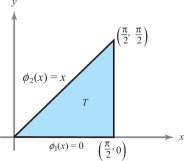
example 1
Find \({\intop\!\!\!\intop}_T\, (x^3 y + \cos x) \,{\it dA}\), where \(T\) is the triangle consisting of all points \((x, y)\) such that \(0\leq x \leq \pi/2, 0 \leq y\leq x\).
solution Referring to Figure 5.25 and formula (1), we have \begin{eqnarray*} &&\intop\!\!\!\intop\nolimits_{T}\, (x^3y + \cos x)\, {\it dA} = \int^{\pi/2}_0 \int^x_0 (x^3 y + \cos x)\, {\it dy}\,{\it dx} \\[5pt] &&\quad = \int^{\pi/2}_0 \bigg[\frac{x^3y^2}{2}+ y \cos x\bigg]^x_{y=0} {\it dx} = \int_0^{\pi/2} \bigg(\frac{x^5}{2} + x \cos x \bigg)\, {\it dx}\\[5pt] &&\quad = \bigg[\frac{x^6}{12}\bigg]^{\pi/2}_0 + \int^{\pi/2}_{0} (x \cos x) \, {\it dx} = \frac{\pi^6}{(12)(64)} + [x \sin x + \cos x]^{\pi/2}_0 \\[5pt] && \quad = \frac{\pi^6}{768} + \frac{\pi}{2} -1. \\[-30pt] \end{eqnarray*}
In the next example, we use formula (1) to find the volume of a solid whose base is a nonrectangular region \(D\).
example 2
Find the volume of the tetrahedron bounded by the planes \(y \,{=}\, 0, z=0, x = 0\), and \(y - x + z = 1\) (Figure \(5.3.7\)).
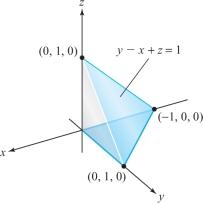
287
solution We first note that the given tetrahedron has a triangular base \(D\) whose points \((x, y)\) satisfy \(-1 \leq x \leq 0\) and \(0 \leq y\leq 1+x\); hence, \(D\) is a \(y\)-simple region. In fact, \(D\) is a simple region; see Figure 5.27.
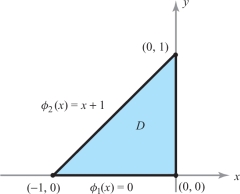
For any point \((x,y)\) in \(D\), the height of the surface \(z\) above \((x, y)\) is \(1 - y + x\). Thus, the volume we seek is given by the integral \[ \intop\!\!\!\intop\nolimits_{D}\, (1-y+x) \,{\it dA}. \]
Using formula (1) with \(\phi_1(x)=0\) and \(\phi_2(x)= x+1\), we have \begin{eqnarray*} \intop\!\!\!\intop\nolimits_{D}\, (1-y+x)\, {\it dA} &=& \int_{-1}^0\, \int_{0}^{1+x}\, (1-y+x)\, {\it dy}\, {\it dx} = \int_{-1}^0\bigg[(1+x)y-\frac{y^2}{2}\bigg]_{y=0}^{1+x} {\it dx} \\ &=& \int_{-1}^{0}\bigg[\frac{(1+x)^2}{2}\bigg]\, {\it dx}= \bigg[\frac{(1+x)^3}{6}\bigg]_{-1}^0=\frac{1}{6}.\\[-30pt] \end{eqnarray*}
example 3
Let \(D\) be a \(y\)-simple region. Describe its area \(A(D)\) as a limit of Riemann sums.
solution If we recall the definition, \(A(D) = {\intop\!\!\!\intop}_D {\it dx}\, {\it dy}\) is the integral over a containing rectangle \(R\) of the function \(f=1\). A Riemann sum \(S_n\) for this integral is obtained by dividing \(R\) into subrectangles and forming the sum \(S_n=\sum_{j,k=0}^{n-1}f^*({\bf c}_{\it jk}) \, \Delta x\,\Delta y\), as in formula (1) of Section 5.3. Now \(f^*({\bf c}_{\it jk})\) is 1 or 0, depending on whether or not \({\bf c}_{\it jk}\) is in \(D\). Consider those subrectangles \(R_{\it jk}\) that have nonvoid intersection with \(D\), and choose \({\bf c}_{\it jk}\) in \(D\cap R_{\it jk}\). Thus, \(S_n\) is the sum of the areas of the subrectangles that meet \(D\) and \(A(D)\) is the limit of these as \(n\to \infty\). Thus, \(A(D)\) is the limit of the areas of the rectangles “circumscribing” \(D\). You should draw a figure to accompany this discussion.
The methods for treating \(x\)-simple regions are entirely analogous. Specifically, we have the following.
Theorem \(4'\) Iterated Integrals for \(x\)-Simple Regions
Suppose that \(D\) is the set of points \((x, y)\) such that \(y\in [c,d]\) and \(\psi_1(y)\leq x\leq \psi_2(y)\). If \(f\) is continuous on \(D\), then \begin{equation*} \intop\!\!\!\intop\nolimits_{D}\, f(x,y)\, {\it dA}= \int_c^d \bigg[ \int_{\psi_{1}(y)}^{\psi_{2}(y)} f(x,y)\, {\it dx} \bigg]\, {\it dy}.\tag{2} \end{equation*}
288
To find the area of \(D\), we substitute \(f = 1\) in formula (2); this yields \[ \intop\!\!\!\intop\nolimits_{D} \ {\it dA}= \int_c^d (\psi_2(y)-\psi_1(y))\, {\it dy} . \]
Again, this result for area agrees with the results of single-variable calculus for the area of a region between two curves.
Either the method for \(y\)-simple or the method for \(x\)-simple regions can be used for integrals over simple regions.
It follows from formulas (1) and (2) that \({\intop\!\!\!\intop}_D f\ {\it dA}\) is independent of the choice of the rectangle \(R\) enclosing \(D\) used in the definition of \({\intop\!\!\!\intop}_D f\ {\it dA}\), because, if we had picked another rectangle enclosing \(D\), we would have arrived at the same formula (1).